[alucard]

Hola tengo el siguiente enunciado.

Con la información proporcionada por el siguiente gráfico, el valor de \( \displaystyle\int_{1}^{\infty}f(x)dx \) es:



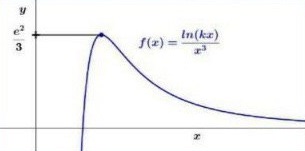
Seleccione una:

\( \circ{}\,\dfrac{2}{3}\qquad\qquad
\circ{}\,2e^{-1}\qquad\qquad
\circ{}\,\dfrac{1}{4}e\qquad\qquad
\circ{}\,1\qquad\qquad
\circ{}\,\dfrac{3}{4} \)

Pude plantear que

\( \displaystyle\int_{1}^{\infty} \dfrac{ln(kx)}{x^3}=\dfrac{1}{4}(ln(k)+1) \)

el problema que encuentro es el como determinar k, dado que cuando hago

\( f(x)=\dfrac{e^2}{3} \)

es imposible despejar x por formas tradicionales , también se me vino a la cabeza el plantear que \( f'(x)=0 \), y con eso hallar el valor del punto en el cual la pendiente vale 0, pero sucede que tampoco puedo despejar la variable x , es posible que este mal el enunciado o hay alguna otra manera de determinar el valor de k que no sea por los caminos que intente?

[Gustavo]

Hola.

también se me vino a la cabeza el plantear que \( f'(x)=0 \), y con eso hallar el valor del punto en el cual la pendiente vale 0, pero sucede que tampoco puedo despejar la variable x

Intenta eso de nuevo: el punto donde se anula la derivada (y donde alcanza el máximo) es \( x=\sqrt[3]{e}/k \).

el problema que encuentro es el como determinar k, dado que cuando hago

\( f(x)=\dfrac{e^2}{3} \)

es imposible despejar x por formas tradicionales

Incluso si despejaras \( x \) en términos de \( k \) no te ayudaría mucho porque lo que tendrías es el valor de \( x \) donde la función \( f_k \) toma el valor \( e^2/3 \) (que no tiene por qué ser el máximo), pero lo que quieres es hallar \( k \) de tal forma que el máximo \( f_k \) sea \( e^2/3 \).

[alucard]

gracias